В теории
гравитации Эйнштейна и в общерелятивистской
электродинамике существуют две качественно
различные категории; пространство-время и
материя. Материя выступает на фоне
пространства-времени, искривляя его. Обе эти
теории используют Риманово пространство и в
обеих теориях гравитационные и электромагнитные
поля носят относительный характер.
Решение программы минимум по
созданию единой теории поля (геометризация
электромагнитного поля) потребовало расширения
специального принципа относительности, на
котором основана электродинамика
Максвелла-Лоренца, до общего принципа
относительности.
С другой стороны, решение
программы максимум (геометризация полей материи)
оказалось возможным благодаря введению в теорию
вращательной относительности, которая указала
на важную роль в явлениях природы торсионных
полей. В механике эти поля проявляют себя как
поля инерции, вызывающие в ускоренных системах
отсчета силы инерции. Пространство событий,
учитывающее вращательную относительность,
наделено структурой геометрии абсолютного
параллелизма с кривизной и кручением, отличными
от нуля, причем роль материальных источников в
новой теории играют все те же торсионные поля.
В теории, построенной с
учетом вращательной относительности, нет двух
категорий (пространства-времени и материальных
источников), а есть только закрученное и
искривленное десятимерное пространство
Вайценбека. Следуя Клиффорду, можно теперь
сказать, что в мире ничего не происходит кроме
изменения кривизны и кручения пространства, поскольку
материальные источники сведены к кручению Риччи.
В качестве полевых уравнений
чисто полевой теории, названной теорией
физического вакуума, выбраны не десять
уравнений типа уравнений Эйнштейна с
геометризированным тензором энергии-импульса
материи, а сорок четыре уравнения, определяющих
структуру геометрии Вайценбека (абсолютного
параллелизма). Эти уравнения описывают
пространственные холмы и вихри, которые
воспринимаются нами как возбужденные состояния
физического вакуума и обнаруживаются нашими
приборами как элементарные частицы материи.
Ранее мы показали
относительную природу гравитационных,
электромагнитных и торсионных полей при
различных координатных преобразованиях, включая
вращательные. Единственным полем, которое ведет
себя как некоторая абсолютная величина, как
относительно поступательных, так и относительно
вращательных координатных преобразований,
оказывается риманова кривизна пространства.
Опыты по рождению частиц из физического вакуума
показывают, что их массы, заряды, спины или
какие-либо другие физические характеристики
относительны, т.е. появляются и исчезают в
процессах рождения из вакуума или ухода в вакуум.
В теории физического вакуума
эти характеристики определяются через риманову
кривизну пространства, поэтому необходимо было
ввести в теорию такой класс систем отсчета, в
которых поле римановой кривизны ведет себя как
относительная величина.

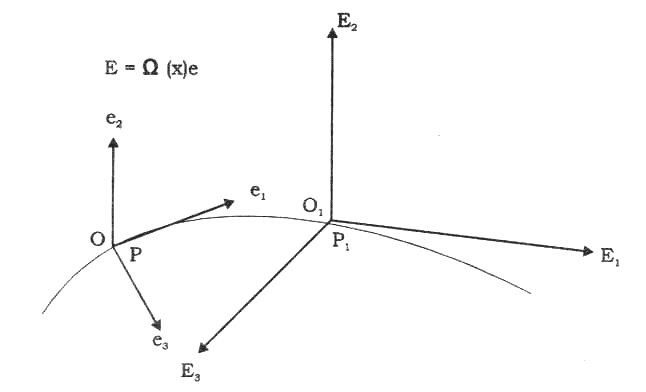
Рис. 14. Конформная система отсчета меняет длину своих базисных векторов по закону Е = W(x)e, где W(х) - масштабный фактор.
Этому требованию удовлетворяют конформные системы отсчета, у которых вектора базиса имеют переменную величину (см. рис.14.), т.е. могут изменяться от точки к точке, а так же в различные моменты времени. В пространстве событий, образованном множеством относительных координат конформных систем отсчета, риманова кривизна становится относительной, поэтому оказываются относительными массы, заряды, спин и другие характеристики вакуумных возбуждений. С помощью конформных координатных преобразований можно описывать процессы рождения и уничтожения элементарных частиц или их взаимные превращения. Например, масса покоя частицы m0 = const при конформных преобразованиях координат становится переменной и меняется по закону m(x) = m0/W(х), где W(х) - масштабный фактор конформных преобразований.
Таблица 2.
| Принцип относительности | Относительная физическая величина | Геометрия пространства событий |
| Галилея-Ньютона | Кинетическая энергия равномерного движения | Евклидово |
| Специальный принцип относительности | Время, длина | Минковского |
| Общий принцип относительности | Гравитационные и электромагнитные поля | Риманово |
| Общий принцип
относительности + вращательная относительность |
Поля материи - торсионные поля | Вайценбека |
| Всеобщая относительность | Массы, заряды, спины и другие топологические характеристики элементарных частиц | Вайценбека-Вейля |
В математике конформная геометрия впервые была предложена немецким математиком Г. Вейлем. Поэтому наиболее богатое по своим свойствам пространство событий с геометрией Вайценбека, дополненное конформными свойствами (пространство Вайценбека-Вейля) больше всего подходит для описания структуры физического вакуума. В таблице 2 наглядно представлено развитие принципа относительности в рамках дедуктивного подхода. Глядя на эту таблицу, можно прийти к заключению, что все в этом мире относительно. Более того, развитие теории относительности потребовало введения нового физического принципа - принципа всеобщей относительности, который утверждает, что все физические поля имеют относительную природу. Задача теоретика состоит в том, чтобы найти такие уравнения физики, в которых все поля относительны. Оказалось, что этому требованию в максимальной степени (на сегодняшний день) удовлетворяют уравнения физического вакуума, построенные на базе структурных уравнений геометрии Вайценбека-Вейля.