В повседневной
жизни мы наблюдаем два типа движений тел -
поступательные и вращательные. Например,
автомобиль, который движется по горизонтальной
поверхности, движется поступательно. Движение
колес автомобиля относительно его корпуса
является вращательным. Поступательное движение
тел описывается в физике поступательными
координатами х, у и z. Для описания
вращательного движения используют вращательные
координаты ф1, ф2,
ф3 (ими могут быть углы
Эйлера).
Механика Ньютона,
электродинамика Максвелла-Лоренца-Эйнштейна,
теория гравитации Эйнштейна и
геометризированная электродинамика построены
так, что используемые этими теориями системы
отсчета образуют множество относительных
поступательных координат (см. таблицу № 1). В
таблице также указаны относительные физические
величины, причем каждая более сложная теория
включает в себя все предыдущие относительные
величины и добавляет свои. Например, в
электродинамике Максвелла-Лоренца-Эйнштейна,
которая использует четырехмерные инерциальные
системы отсчета, кинетическая энергия
равномерного движения зарядов относительна, так
же как и в механике Ньютона. Но в ней
дополнительно оказываются относительными длина
объекта и время его жизни. В теории гравитации
Эйнштейна и геометризированной электродинамике
относительно все то, что и в электродинамике
Максвелла-Лоренца-Эйнштейна, плюс
относительными оказываются гравитационные и
электромагнитные поля соответственно.
Таблица № 1.
| Теория | Система отсчета | Относительные координаты | Геометрия многообразия относительных координат | Относительная физическая величина |
| Механика Ньютона | Трехмерная инерциальная | x, y, z | Трехмерная евклидова | Кинетическая энергия равномерного движения |
| Электродинамика Максвелла- Лоренца- Эйнштейна | Четырехмерная инерциальная | x, y, z, ct | Четырехмерная псевдоевклидова | Длина и время |
| Теория гравитации Эйнштейна | Ускоренная локально- инерциальная первого рода | x, y, z, ct | Четырехмерная риманова | Гравитационное поле |
| Геометризированная электродинамика | Ускоренная локально- инерциальная первого рода | x, y, z, ct | Четырехмерная риманова | Электромагнитное поле |
Легко видеть, что в
эту таблицу не входят вращательные координаты ф1,
ф2, ф3.
Это и понятно, поскольку все перечисленные в
таблице системы отсчета по определению не
вращаются. Поэтому можно сказать, что до сих пор
теория относительности развивалась как теория
поступательной относительности.
Следующий шаг в развитии
теории относительности потребовал введения
многообразия относительных координат
ускоренных систем отсчета, которые испытывают
вращение при своем движении. Такие системы
отсчета движутся не только в трансляционных
координатах, но также и во вращательных. Теория, в
которой используются вращательные координаты,
требует увеличения размерности пространства
событий. Например, если рассматриваются
трехмерные вращающиеся системы отсчета с
трансляционными координатами х, у и z, то они
дополнительно описываются тремя вращательными
координатами. В этом случае пространство событий
шестимерно. Если же мы будем рассматривать
четырехмерные вращающиеся системы отсчета, то
пространство событий будет уже десятимерным,
поскольку в четырехмерном пространстве
трансляционных координат х, у, z, ct имеется шесть
вращательных координат: три пространственных
угла ф1, ф2,
ф3 и три псевдоевклидовых
угла q1, q2, q3.
Трансляционные и
вращательные координаты существенно отличаются
по своим свойствам. Трансляционные координаты
относятся к классу голономных (или
интегрируемых). Движение в голономных
координатах характерно тем, что оно не
зависит от направления пути в одну и ту
же точку пространства.

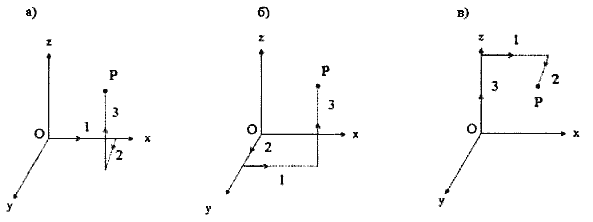
Рис. 8. Результат движения в голономных координатах х, у, и z не завит от последовательности пути движения.
Наглядно это
свойство изображено на рис. 8, где показано
движение в голономных координатах х, у,
и z из начала координат О до точки Р по
отрезкам 1, 2 и 3 вдоль осей Ох, Оу и Oz. Ha рис. 8 а)
движение начинается вдоль оси х на
величину отрезка 1, затем вдоль оси у на
величину отрезка 2 и, наконец, вдоль оси z
на величину отрезка 3. В результате мы приходим в
точку Р. На рис. 8 б) порядок движения
изменился: сначала движение происходит вдоль оси
у на величиау отрезка 2, затем вдоль оси х
на величину отрезка 1 и, окончательно, вдоль оси z
на величину отрезка 3. И опять мы приходим в точку
Р. Этот же результат мы получим, если начнем
движение вдоль оси z, как это показано на
рис. 8 в).
В отличие от голономных
координат х, у, и z, при
движении в неголономных координатах ф1,
ф2, ф3
результат двух поворотов на конечные углы
зависит от последовательности этих поворотов.
Для иллюстрации этого утверждения, рассмотрим
два последовательных поворота вокруг осей х, и z
на углы 90° (рис. 9 и 10).
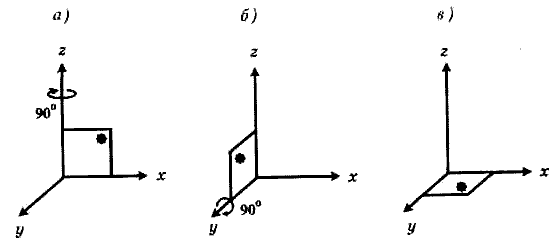
Рис. 9. Два последовательных поворота на угол 180°: а) - поворот на 90° по часовой стрелке вокруг оси z; б) - то же, вокруг оси у; в) - результат двух последовательных поворотов.
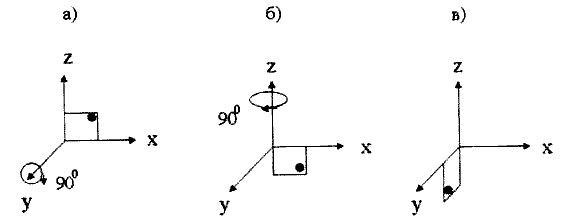
Рис. 10. Смена порядка последовательных поворота на угол 180°: а) -поворот на 90° по часовой стрелке вокруг оси у, б) - то же, вокруг оси z; в) - результат двух последовательных поворотов.
Из рисунков видно, что результат двух конечных поворотов вокруг осей у и z зависит от последовательности этих поворотов (положения квадрата со звездочкой на рис. 9 в и рис. 10 в не совпадают).